|
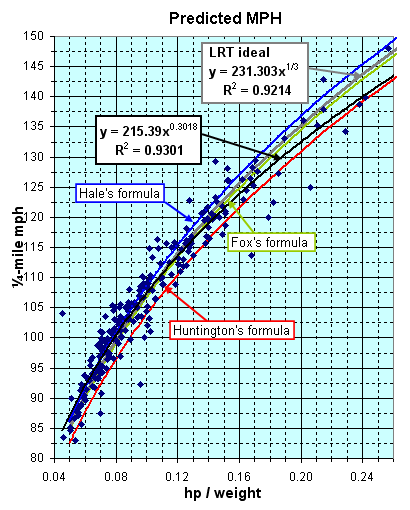
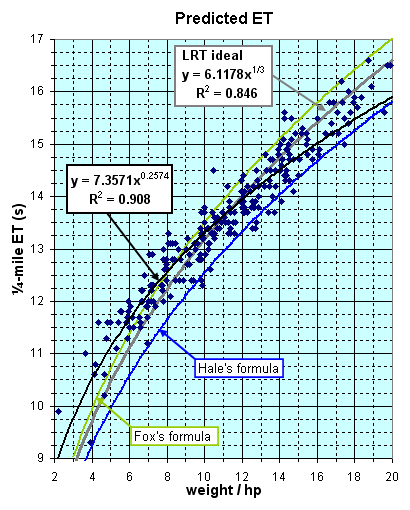
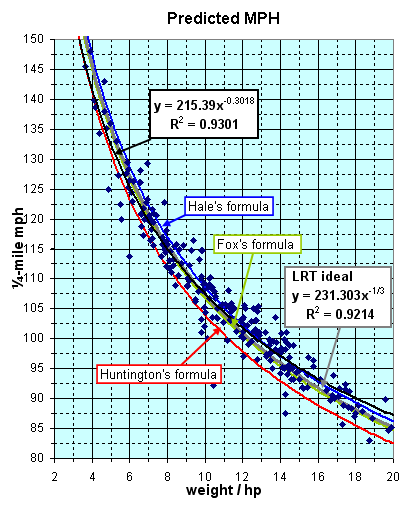
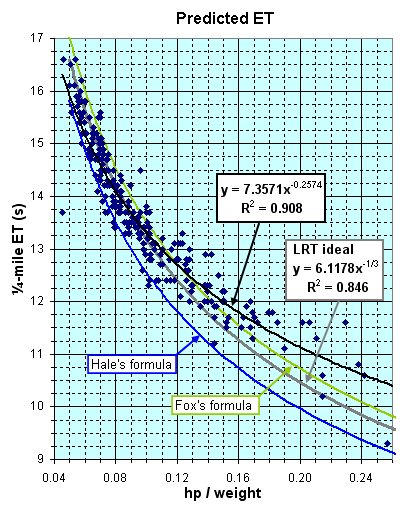
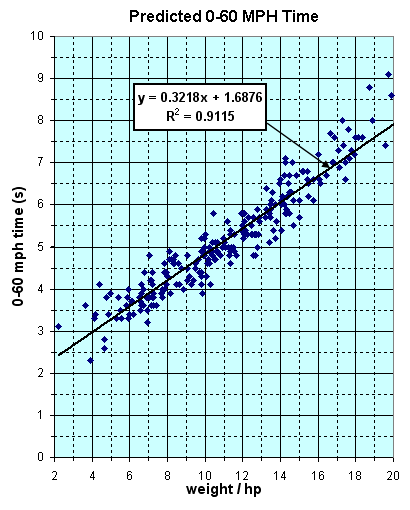
"... The constant is 224 not 225, and MPH is calculated by dividing 224 by the cube root of the lbs.-per-HP ratio ... .
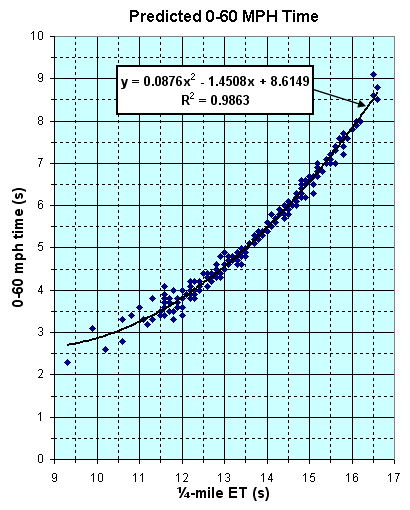
"... It was the result of 40 or 50 road and strip tests of many different cars. What I would do is test the car with an accelerometer - and several complex equations - to determine the true peak HP delivered at the clutch under accelerating conditions, usually in a gear giving the HP peak between 60 and 90 mph, to make it easier to get consistent accelerometer readings. (The gear effect was compensated by using a factor to allow for engine and drive line rotating inertia.) Anyway, the car was tested on a quarter-mile to accurately determine the terminal speed at the end of the quarter. Using the gross weight of the car and the tested true clutch HP, the lbs-per-HP ratio was derived ... and this was plotted on a graph vs. trap speed. The above formula is the average line through the plotted points. And actually there was amazing correlation. "Note that I only tested cars with trap speeds between 70 and 115 mph. The curve is extrapolated above 115 mph. "Incidentally, I did the same thing with a formula for quarter-mile e.t. That one is a constant of 6.29 times the cube root of the lbs.-per-HP ratio. However, there was more scatter in the plotted points here, due to wider variations in traction between cars. Minimum tested e.t. was 12 seconds. "Anyway, I know I was the first to derive ths type of equation, based on true net HP. It represented many hours of work and tedious slide rule calculations over a period of 10 years." |
| Goodness of Fit (R2) | ||||
|---|---|---|---|---|
| Predicted MPH | Predicted ET | |||
| Huntington | 0.8553 | 0.7693 | ||
| Fox | 0.9193 | 0.7870 | ||
| Hale | 0.9124 | 0.6234 | ||
| LRT "ideal" | 0.9214 | 0.8465 | ||
| LRT "best fit" | 0.9301 | 0.9076 | ||




|
The LRT Formulas |
|
Patrick Hale's Formulas |
|
Geoffrey Fox's Formulas |
| Comparison of Formula Estimates and Actual Track Performance | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3000GT VR4 / Stealth R/T TT weighing 3900 lbs with driver | ||||||||
| LRT | Fox | Hale | Typical ranges | |||||
| hp | ET | mph | ET | mph | ET | mph | ET | mph |
| 320 | 14.003 | 101.27 | 14.427 | 99.94 | 13.405 | 101.68 | 14.2 - 13.4 | 99 - 102 |
| 350 | 13.684 | 104.05 | 14.002 | 102.97 | 13.011 | 104.77 | 13.5 - 13.0 | 103 - 105 |
| 400 | 13.221 | 108.33 | 13.393 | 107.66 | 12.444 | 109.53 | 13.3 - 12.5 | 107 - 109 |
| 450 | 12.827 | 112.25 | 12.877 | 111.97 | 11.965 | 113.92 | 12.9 - 12.0 | 111 - 114 |
| 500 | 12.483 | 115.88 | 12.433 | 115.97 | 11.552 | 117.99 | 12.2 - 11.7 | 115 - 118 |
| 550 | 12.181 | 119.26 | 12.044 | 119.72 | 11.191 | 121.80 | 12.1 - 11.3 | 118 - 122 |
| 600 | 11.911 | 122.43 | 11.700 | 123.24 | 10.871 | 125.38 | 11.5 - 11.2 | 122 - 125 |
| 650 | 11.668 | 125.42 | 11.392 | 126.57 | 10.585 | 128.78 | 11.2 - 11.0 | 125 - 128 |
| 700 | 11.448 | 128.26 | 11.114 | 129.74 | 10.326 | 132.00 | 11.0 - 10.8 | 128 - 132 |
| 750 | 11.246 | 130.96 | 10.861 | 132.76 | 10.092 | 135.07 | 10.787 | 133.9 |
| 800 | 11.061 | 133.53 | 10.630 | 135.64 | 9.877 | 138.00 | 10.561 | 135.5 |
| Back | Home | Forward |